Das Vektorprodukt

Mit der Definition des Skalarprodukts besitzt man eine rechnerische Möglichkeit, zu einem vorgegebenen Vektor einen anderen Vektor zu finden, der auf dem ersten Vektor senkrecht steht.

Denkt man diese Vorgehensweise zu Ende, dann landet man bei der Konstruktion eines Koordinatensystems:

Alles was man dazu braucht sind drei Vektoren, die paarweise aufeinander senkrecht stehen. (Anschliessend muss man sie normieren auf Länge 1 L.E.)

Machen wir uns ans Werk:

Vorgegeben sind zwei Vektoren \(\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\\\end{pmatrix}\) und \(\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\\\end{pmatrix}\).

Gesucht ist ein Vektor \(\vec{c}=\begin{pmatrix}c_1\\c_2\\c_3\\\end{pmatrix}\) mit \(\vec{a}\perp\vec{c}\) und \(\vec{b}\perp\vec{c}\), also \(\vec{a}\cdot\vec{c}=0\) und \(\vec{b}\cdot\vec{c}=0\).

Damit ergibt sich das Gleichungssystem mit den Unbekannten \(c_1,\,c_2,\,c_3\):

\[\begin{matrix} a_1 \cdot c_1 & + & a_2 \cdot c_2 & + & a_3 \cdot c_3 & = & 0\\ b_1 \cdot c_1 & + & b_2 \cdot c_2 & + & b_3 \cdot c_3 & = & 0\\ \end{matrix}\]

Dieses Gleichungssystem hat unendlich viele Lösungen, denn es ist unterbestimmt (zwei Gleichungen, drei Unbekannte).
Eine mögliche (und möglichst einfache) Lösung ist

\[c_1=a_2\,b_3-a_3\,b_2,\; c_2=a_3\,b_1-a_1\,b_3,\; c_3=a_1\,b_2-a_2\,b_1\]

(Bitte nachrechnen!)

Also ist ein möglicher Lösungsvektor

\[\vec{c}= \begin{pmatrix} a_2\,b_3 - a_3\,b_2 \\ a_3\,b_1 - a_1\,b_3 \\ a_1\,b_2 - a_2\,b_1 \end{pmatrix}\]

Die Verknüpfung, die zwei Vektoren diesen dritten Vektor zuordnet heißt Vektorprodukt.

Definition:

Sind \(\vec{a}=\begin{pmatrix}a_1\\a_2\\a_3\\\end{pmatrix}\) und \(\vec{b}=\begin{pmatrix}b_1\\b_2\\b_3\\\end{pmatrix}\) zwei Vektoren aus \({\mathbb{R}^3}\), so ist das Vektorprodukt aus \(\vec{a}\) und \(\vec{b}\) definiert als:

\[\vec{a}\times\vec{b}= \begin{pmatrix} a_2\,b_3 - a_3\,b_2 \\ a_3\,b_1 - a_1\,b_3 \\ a_1\,b_2 - a_2\,b_1 \end{pmatrix}\]

Drehsinn

Anschaulich ist der Vektor \(\vec{c}\) also ein Vektor, der auf den Vektoren \(\vec{a}\) und \(\vec{b}\) senkrecht steht.
Die Vektoren bilden zusammen ein Rechtssystem!
Genauer bedeutet das Folgendes: Zwei beliebige verschiedene Vektoren spannen im \({\mathbb{R}^3}\) eine Ebene auf. Ein Vektor \(\vec{c}\), der auf dieser Ebene und damit auch auf den aufspannenden Vektoren senkrecht steht, kann entweder “nach oben” oder “nach unten” zeigen (von der Ebene aus betrachtet).
Welchen der beiden rechnet man denn mit dem Vektorprodukt aus?
Nun, gerade denjenigen der beiden, der mit den beiden aufspannenden Vektoren ein Rechtsschraubsystm bildet:

1.) Daumen der rechten Hand
2.) Zeigefinger der rechten Hand
3.) Mittelfinger der rechten Hand (Zeigt in Richtung des Vektorprodukts)

Die Richtung nach “unten” erhält man dann durch \(-\vec{c}\)

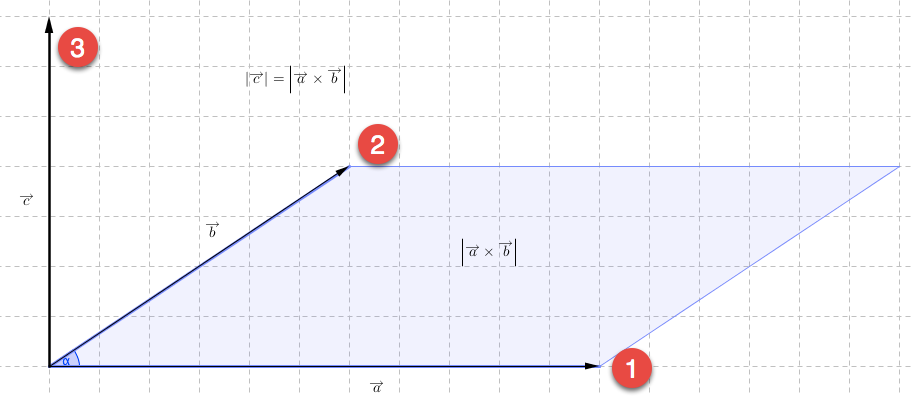
Was bedeutet die Länge \(c = \left| {\overrightarrow c } \right|\)

Die Richtung des Vektors haben wir jetzt geklärt, aber welche Bedeutung hat sein Betrag? Es stellt sich heraus, dass die Länge des Vektors \(\vec{c}\) gerade die Masszahl für die Fläche des von \(\vec{a}\) und \(\vec{b}\) aufgespannten Parallelogramms ist.
Das liefert eine schöne Möglichkeit, mit dem Vektorprodukt Flächeninhalte (und damit auch Volumeninhalte) zu berechnen!

Merkregel: Betrag von \(\vec{c}\) = Fläche des Parallelogramms

Beweis:

(Zum selber Nachrechnen - dringend empfohlen)

Der Flächeninhalt des besagten Parallelogramms beträgt (siehe Unterricht):

\[A=\left|\vec{a}\right|\cdot\left|\vec{b}\right|\cdot\sin(\varphi)\]

Wir müssen also zeigen, dass

\[\left|\vec{c}\right|=\left|\vec{a}\right|\cdot\left|\vec{b}\right|\cdot\sin(\varphi)\]

Quadrieren liefert:

\[\begin{array}{rcl} \left[\left|\vec{a}\right|\cdot\left|\vec{b}\right|\cdot\sin(\varphi)\right]^2 & = & \left|\vec{a}\right|^2\cdot\left|\vec{b}\right|^2\cdot\sin^2(\varphi)\\ & = & \left|\vec{a}\right|^2\cdot\left|\vec{b}\right|^2\cdot\left(1-\cos^2(\varphi)\right)\\ & = & \left|\vec{a}\right|^2\cdot\left|\vec{b}\right|^2- \left|\vec{a}\right|^2\cdot\left|\vec{b}\right|^2\cdot\cos^2(\varphi)\\ & = & \left|\vec{a}\right|^2\cdot\left|\vec{b}\right|^2-\left(\vec{a}\circ\vec{b}\right)^2\\ & = & \left(a_1^2+a_2^2+a_3^2\right)\cdot\left(b_1^2+b_2^2+b_3^2\right)- \left(a_1\,b_1+a_2\,b_2+a_3\,b_3\right)^2\\ \end{array}\]

Mühsames Ausmultiplizieren, Zusammenfassen und Umsortieren liefert:

\[\begin{array}{rcl} \left[\left|\vec{a}\right|\cdot\left|\vec{b}\right|\cdot\sin(\varphi)\right]^2 & = & \underbrace{a_2^2\,b_3^2-2\,a_2\,a_3\,b_2\,b_3+a_3^2\,b_2^2}_{=(a_2\,b_3-a_3\,b_2)^2}\\ & &\qquad+\underbrace{a_3^2\,b_1^2-2\,a_1\,a_3\,b_1\,b_3+a_1^2\,b_3^2}_{=(a_3\,b_1-a_1\,b_3)^2}\\ & & \qquad\qquad+\underbrace{a_1^2\,b_2^2-2\,a_1\,a_2\,b_1\,b_2+a_2^2\,b_1^2}_{=(a_1\,b_2-a_2\,b_1)^2}\\ & = & \left(a_2\cdot b_3-a_3\cdot b_2\right)^2 + \left(a_3\cdot b_1-a_1\cdot b_3\right)^2 + \left(a_1\cdot b_2-a_2\cdot b_1\right)^2\\ & = & \left|\vec{a}\times\vec{b}\right|^2\\ & = & \left|\vec{c}\right|^2\\ \end{array}\]

Da

\[\varphi\in\left[0^{\circ};180^{\circ}\right]\] also \[\sin(\varphi)\ge0\] gilt auch: \[\left|\vec{c}\right|=\left|\vec{a}\right|\cdot\left|\vec{b}\right|\cdot\sin(\varphi)\]

Merkregel für das Kreuzprodukt

Man erkennt sehr gut, wieso das Kreuzprodukt so heisst :-)

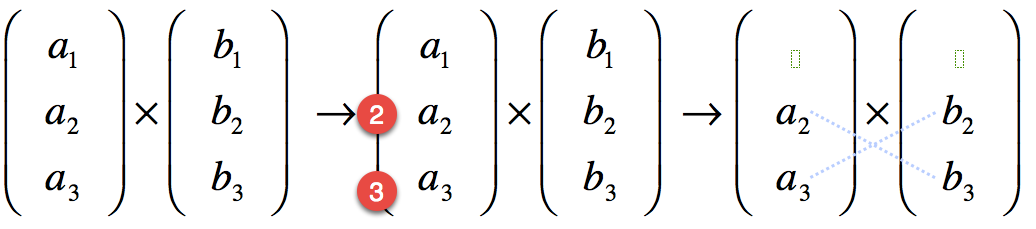
Für die erste Komponente die erste Zeile streichen, dann überkreuz multiplizieren und die Produkte voneinander abziehen: \[a_2\,b_3 - a_3\,b_2\]

Für die zweite Komponente die zweite Zeile streichen, dann überkreuz multiplizieren und die Produkte voneinander abziehen: \[a_1\,b_3 - a_3\,b_1\]

Zusätzlich: Das Vorzeichen umdrehen: \[-(a_1\,b_3 - a_3\,b_1)=a_3\,b_1 - a_1\,b_3\]

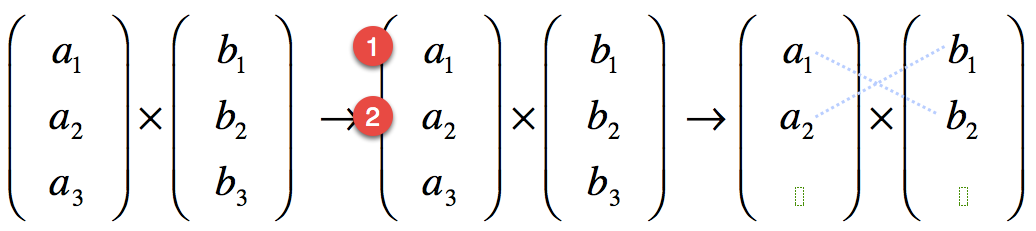
Für die dritte Komponente die dritte Zeile streichen, dann überkreuz multiplizieren und die Produkte voneinander abziehen: \[a_1\,b_2 - a_2\,b_1\]