Das Spatprodukt
Die Links - Rechts - Kombination aus Vektorprodukt und Skalarprodukt liefert eine sehr einfache Formel zur Berechnung des Volumens von Pyramiden oder Spaten - umgangssprachlich könnte man einen Spat als “schiefen” Quader betrachten, dessen Seiten nur Parallelogramme sein brauchen.
Man nennt einen solchen Körper ein (gerades, wenn rechtwinklig) schiefes Prisma bzw. Spat.
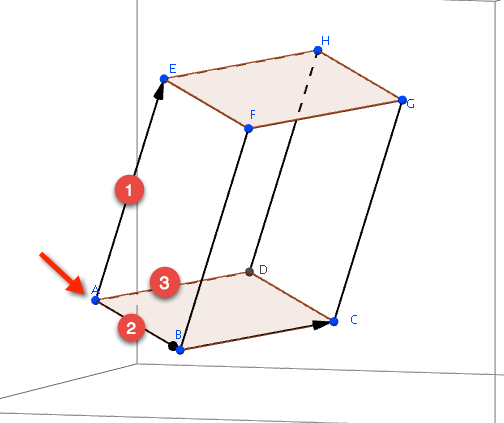
Anwendung des Spatproduktes:
Man wähle eine Ecke des Spats aus (hier A)!
Man bestimme drei i. a. verschiedene Kantenvektoren, die von A ausgehen: \(\vec{AB}\), \(\vec{AD}=\vec{BC}\), \(\vec{AE}\).
Man berechne:
\[V = \left| {\left( {\vec {AB} \times \vec {AD}} \right) \circ \vec {AE}} \right|\]
- Da nur der Betrag gefragt ist, spielt die Reihenfolge der Vektoren keine Rolle (Wie auch, würde ja bedeuten, dass sich das Volumen ändert, wenn man den Spat umdreht und anders bezeichnet!)
Übrigens:
Für eine von den drei Vektoren \(\vec{AB}\), \(\vec{AD}\) und \(\vec{AE}\) aufgespannte Pyramide gilt dann
\[V = \frac{1}{6} \cdot \left| {\left( {\vec {AB} \times \vec {AD}} \right) \circ \vec {AE}} \right|\]
Die Herleitung kurz zusammengefasst:
Das Volumen des Prismas berechnet sich durch die Formel Grundfläche x Höhe: Prinzip von Cavalieri
Die Grundfläche des Prismas ist ein Parallelogramm. Dessen Flächeninhalt erhält man aus dem Vektorprodukt der Seitenvektoren \(\vec{a}\) und \(\vec{b}\): \(G =\left| \vec{a}\times\vec{b} \right|\)
Die Höhe erhält man aus dem Pythagoras im Höhendreieck. \(h = \sin (\beta ) \cdot b\)
Der Clou: \(\alpha = 90° - \beta\) ist gerade der Winkel zwischen \(\vec{a}\times\vec{b}\) und \(\vec{c}\), so dass man für das Volumen erhält:
\[V = G \cdot h = \left| {\vec a \times \vec b} \right| \cdot c \cdot \cos (\alpha ) = \left| {\left( {\vec a \times \vec b} \right) \circ \vec c} \right|\]